Directions: Each GMAT Data Sufficiency problem consists of a question and two statements labeled (1) and (2), that provide data. Based on the data given plus your knowledge of mathematics and everyday facts, you must decide whether the data are sufficient for answering the question. The five answer choices are the same for every data sufficiency question.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
A new Coffee Bean & Tea Leaf coffee drink consists only of certain amounts of espresso and sugar. What is the ratio of espresso to sugar in the new drink?
(1) There are 15 ounces of sugar in 35 ounces of the new drink.
(2) There are 40 ounces of espresso in 70 ounces of the new drink.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 1 Explanation:
The correct response is (D). We do not need to know the exact amount of espresso and sugar in the new drink. We only need to know the relationship between the amounts, since this question only asks for the ratio of espresso to sugar in the new drink.
If you chose (A), remember that we can find the ratio between ingredients as soon as we know the amount of each ingredient in the beverage or if we know the amount of one ingredient in relation to the set amount of the drink (part to part , or one part to whole). Since there are only two ingredients in the new drink, 20 ounces must be espresso. The ratio in (1) would be 20:15, or 4:3. However, (B) is also sufficient, since 30 ounces would be sugar.
If you chose (B), since the new drink consists only of espresso and sugar, we can find the ratio of espresso to sugar. The 30 ounces difference here must be made up of sugar. Therefore, the ratio is 40:30, or 4:3.
If you chose (C), you failed to recognize that each statement alone is sufficient. This is because the question is asking only for a ratio. We don’t need all of the “real-world” values to come up with a ratio, only the part-to-part or part-to-whole in a given circumstance to express the ratio. Each statement is sufficient to do this.
If you chose (E), you missed the idea that you can figure out the amount of espresso and the amount of sugar for a given amount of the new drink based on either statement (you just need to subtract).
If you chose (A), remember that we can find the ratio between ingredients as soon as we know the amount of each ingredient in the beverage or if we know the amount of one ingredient in relation to the set amount of the drink (part to part , or one part to whole). Since there are only two ingredients in the new drink, 20 ounces must be espresso. The ratio in (1) would be 20:15, or 4:3. However, (B) is also sufficient, since 30 ounces would be sugar.
If you chose (B), since the new drink consists only of espresso and sugar, we can find the ratio of espresso to sugar. The 30 ounces difference here must be made up of sugar. Therefore, the ratio is 40:30, or 4:3.
If you chose (C), you failed to recognize that each statement alone is sufficient. This is because the question is asking only for a ratio. We don’t need all of the “real-world” values to come up with a ratio, only the part-to-part or part-to-whole in a given circumstance to express the ratio. Each statement is sufficient to do this.
If you chose (E), you missed the idea that you can figure out the amount of espresso and the amount of sugar for a given amount of the new drink based on either statement (you just need to subtract).
Question 2 |
How many in a group are women with blue eyes?
(1) Of the women in the group, 5 percent have blue eyes.
(2) Of the men in the group, 10 percent have dark-colored eyes.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 2 Explanation:
The correct response is (E). There are three numbers we must know in order to find the percent of women with blue eyes: number of men in the group, number of women in the group, number of women with blue eyes.
If you chose (A), we know that 5% of the women have blue eyes, but we do not know how many members of the group are women, thus we cannot answer the question.
If you chose (B), this only gives us information on the men in the group, but the question concerns the number of women who fit a certain criteria.
If you chose (C), the information in the second statement does not tell us anything about the women in the group, and the first statement only tells us the percentage with blue eyes, not enough to determine the actual number.
If you chose (D), both statements are insufficient for different reasons. Statement (1) tells us the percentage, but not the actual number of women in the group, so we cannot turn that percentage into a number as this “value” question requires. Statement (2) does not relate at all to the women in the group and is therefore insufficient.
If you chose (A), we know that 5% of the women have blue eyes, but we do not know how many members of the group are women, thus we cannot answer the question.
If you chose (B), this only gives us information on the men in the group, but the question concerns the number of women who fit a certain criteria.
If you chose (C), the information in the second statement does not tell us anything about the women in the group, and the first statement only tells us the percentage with blue eyes, not enough to determine the actual number.
If you chose (D), both statements are insufficient for different reasons. Statement (1) tells us the percentage, but not the actual number of women in the group, so we cannot turn that percentage into a number as this “value” question requires. Statement (2) does not relate at all to the women in the group and is therefore insufficient.
Question 3 |
On a soccer team, one team member is selected at random to be the goalie. What is the probability that a substitute player will be the goalie?
(1) One-sixth of the team members are substitute players.
(2) 18 of the team members are not substitute players.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 3 Explanation:
The correct response is (A). The probability that a substitute will be chosen can be found if we know the ratio of substitutes to total members OR if we know both values exactly. Here we are given the ratio = 1/6, so it is sufficient. If you chose (B), we know 18 are NOT substitutes, but we do not know how many ARE substitutes, so we cannot determine the probability.
Question 4 |
A designer purchased 20 mannequins that each cost an equal amount and then sold each one at a constant price. What was the designer’s gross profit on the sale of the 20 mannequins?
(1) If the selling price per mannequin had been double what it was, the gross profit on the total would have been $2400.
(2) If the selling price per mannequin had been $2 more, the store's gross profit on the total would have been $440.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 4 Explanation:
The correct response is (B). This question asks about gross profit, which we know is derived from subtracting the total cost from the total selling price. If we know the cost of each mannequin and the selling price of each mannequin we can determine the designer’s gross profit. From the given information, we can write the following equation: P = 20 (s – c), where s = selling price and c = cost. So either we’ll need a value for s and a value for c, or we’ll need the value of (s – c).
Statement (1) tells us that $2400 = (20(2s – c)) or 2400 = 40s – 20c. We can divide both sides by 20 and simplify the equation to get: 120 = 2s – c. We still don’t know s and c. Insufficient.
Statement (2) tells us that 440 = 20(s + 2 – c). Let’s simplify:
440 = 20s + 40 – 20c
400 = 20s – 20c
400 = 20 (s – c)
Sufficient. Even though we didn’t solve for s and c separately, we were able to find the value of (s – c).
Statement (1) tells us that $2400 = (20(2s – c)) or 2400 = 40s – 20c. We can divide both sides by 20 and simplify the equation to get: 120 = 2s – c. We still don’t know s and c. Insufficient.
Statement (2) tells us that 440 = 20(s + 2 – c). Let’s simplify:
440 = 20s + 40 – 20c
400 = 20s – 20c
400 = 20 (s – c)
Sufficient. Even though we didn’t solve for s and c separately, we were able to find the value of (s – c).
Question 5 |
A shopping center increased its revenues by 10% between 2010 and 2011. The shopping center’s costs increased by 8% during the same period. What is the firm's percent increase in profits over this period, if profits are defined as revenues minus costs?
(1) The firm's initial profit is $200,000.
(2) The firm's initial revenues are 1.5 times its initial costs.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 5 Explanation:
The correct response is (B). Let’ start with our most basic Profit formula: Profit = Revenue – Cost.
Using Statement (1), we can say that 200,000 = R – C.
Profit in 2010 = R – C
Profit in 2011 = 1.1R – 1.08C
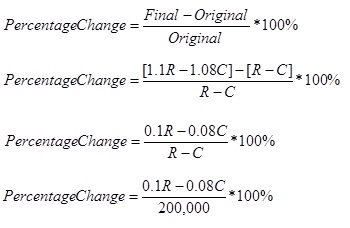
Without knowing R or C, we cannot determine the percentage change in this case. Notice that if we knew R or some other relationship between R and C, we could substitute into the equation R-C =200,000 to solve for the missing piece.
Statement 1 is insufficient.
Using Statement (2), R=1.5C
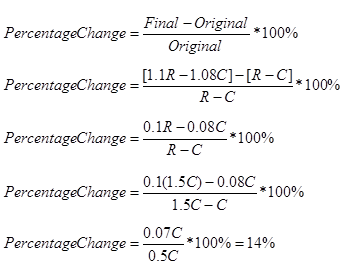
The last step was not necessary if you realized that substituting R=1.5C into the expression for calculating the percentage change will give you an expression in which the Cs cancel out, giving you an actual percentage.
Statement 2 is sufficient.
Using Statement (1), we can say that 200,000 = R – C.
Profit in 2010 = R – C
Profit in 2011 = 1.1R – 1.08C
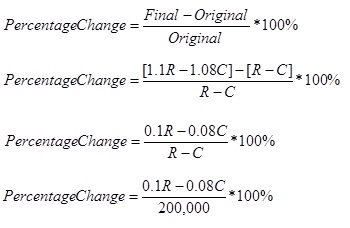
Without knowing R or C, we cannot determine the percentage change in this case. Notice that if we knew R or some other relationship between R and C, we could substitute into the equation R-C =200,000 to solve for the missing piece.
Statement 1 is insufficient.
Using Statement (2), R=1.5C
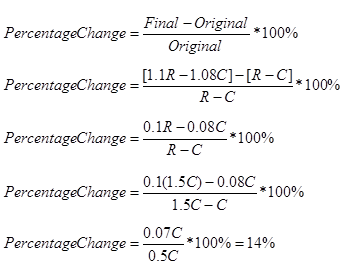
The last step was not necessary if you realized that substituting R=1.5C into the expression for calculating the percentage change will give you an expression in which the Cs cancel out, giving you an actual percentage.
Statement 2 is sufficient.
Question 6 |
A certain number is not an integer. Is the number less than .4?
(1) The number rounded to the nearest tenth is .4.
(2) The number rounded to the nearest integer is 0.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 6 Explanation:
If you chose (A), we know the “nearest” tenth is .4, so this means the number is between .35 and .45. If it were smaller than .35 (for example, .34), we would round down to .3, and if it were greater than .45 (for example, .47), we would round up to .5. Since .4 is between .35 and .45, we can’t tell if the value of the number is less than or greater than (or equal to) .4.
If you chose (B), we know the “nearest” integer is 0, so the number must be between -0.5 and .5. While most of the values in this range are less than .4, the values between .4 and .5 are greater than .4.
If you chose (C), remember we can express the information from the first statement as an inequality: .35 ≤ x < .45. And we can express the information from the second statement as an inequality: -0.5 < x < .5. Since the range of values for the first inequality is within the range of the second inequality, the range of values that satisfy both inequalities will be the same as the range of values in the first inequality (.35 ≤ x < .45). Since we already determined that the first inequality is not sufficient, combining both inequalities will not be sufficient.
If you chose (D), you may have missed the possible values between .4 and .45 in Statement 1, and the range of possible values between .4 and .5 in Statement 2.
(E) is the correct response. Even combined, we get a range between .35 and .45. There are values that are possible both above and below (and equal to) .4.
If you chose (B), we know the “nearest” integer is 0, so the number must be between -0.5 and .5. While most of the values in this range are less than .4, the values between .4 and .5 are greater than .4.
If you chose (C), remember we can express the information from the first statement as an inequality: .35 ≤ x < .45. And we can express the information from the second statement as an inequality: -0.5 < x < .5. Since the range of values for the first inequality is within the range of the second inequality, the range of values that satisfy both inequalities will be the same as the range of values in the first inequality (.35 ≤ x < .45). Since we already determined that the first inequality is not sufficient, combining both inequalities will not be sufficient.
If you chose (D), you may have missed the possible values between .4 and .45 in Statement 1, and the range of possible values between .4 and .5 in Statement 2.
(E) is the correct response. Even combined, we get a range between .35 and .45. There are values that are possible both above and below (and equal to) .4.
Question 7 |
What is the area of a triangle (with vertices at FCE) that is inscribed in a hexagon with vertices at ABCDE?
(1) The hexagon is regular and BE = 14.
(2) EC = 7√3.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 7 Explanation:
(A) is the correct response.
Statement 1:
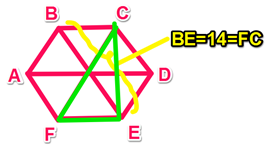
A regular hexagon can be divided into six equilateral triangles, each with a central angle measure of 60 degrees. Remember that we can inscribe a regular hexagon in a circle such that each vertex is a point on the circumference of the circle. Central Angle Theorem states that the central angle in a circle is always twice an inscribed angle when the point of the inscribed angle (in this case point C) is on the major arc. For this figure, this means angle FCE = 30. Since angle CFE = 60, we have a 30-60-90 triangle. If BE = 14, then FC = 14 as well. We’d now be able to solve for the height (CE) and base (FE) using the 30-60-90 side ratios. Since this is a data sufficiency question, we can stop here and conclude that statement 1 is sufficient.
However, if you actually had to calculate the area of triangle FCE, here is how you might proceed: The sides of a 30-60-90 are in the ratio 1 : √3 : 2 , so the sides of triangle FCE will have the following lengths: FE = 7, CE= 7√3 , FC=14.
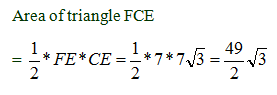
Statement 2:
If the hexagon is regular, we can calculate the area of triangle FCE using a process similar to the one illustrated above. However, statement 2 does not tell us that the hexagon is regular. If the hexagon is not regular, we can come up with different areas for triangle FCE, depending on what we assume. Statement 2 alone is not sufficient.
Statement 1:

A regular hexagon can be divided into six equilateral triangles, each with a central angle measure of 60 degrees. Remember that we can inscribe a regular hexagon in a circle such that each vertex is a point on the circumference of the circle. Central Angle Theorem states that the central angle in a circle is always twice an inscribed angle when the point of the inscribed angle (in this case point C) is on the major arc. For this figure, this means angle FCE = 30. Since angle CFE = 60, we have a 30-60-90 triangle. If BE = 14, then FC = 14 as well. We’d now be able to solve for the height (CE) and base (FE) using the 30-60-90 side ratios. Since this is a data sufficiency question, we can stop here and conclude that statement 1 is sufficient.
However, if you actually had to calculate the area of triangle FCE, here is how you might proceed: The sides of a 30-60-90 are in the ratio 1 : √3 : 2 , so the sides of triangle FCE will have the following lengths: FE = 7, CE= 7√3 , FC=14.
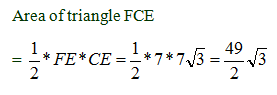
Statement 2:
If the hexagon is regular, we can calculate the area of triangle FCE using a process similar to the one illustrated above. However, statement 2 does not tell us that the hexagon is regular. If the hexagon is not regular, we can come up with different areas for triangle FCE, depending on what we assume. Statement 2 alone is not sufficient.
Question 8 |
How many integers are there between m and n, exclusive, if m and n are themselves integers?
(1) m − n = 8
(2) There are 5 integers between, but not including, m − 1 and n − 1.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 8 Explanation:
The correct response is (D). This question is provides a great opportunity to try out numbers.
Statement 1: Let’s say m = 9 and n = 1, then m – n = 9 – 1 = 8. There are 7 integers between 1 and 9. If we choose a different set of integers: let’s say m = -2 and n = -10. There are still 7 integers between these two numbers.
Statement 2: If there are 7 integers between m -1 and n -1, then there will still be 7 integers between m and n. This is sufficient for the same reason that statement 1 was sufficient.
Statement 1: Let’s say m = 9 and n = 1, then m – n = 9 – 1 = 8. There are 7 integers between 1 and 9. If we choose a different set of integers: let’s say m = -2 and n = -10. There are still 7 integers between these two numbers.
Statement 2: If there are 7 integers between m -1 and n -1, then there will still be 7 integers between m and n. This is sufficient for the same reason that statement 1 was sufficient.
Question 9 |
For integers w, x, y, and z, is wxyz = -1?
(1) wx / yz = -1
(2) w = -1/x and y = 1/z
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 9 Explanation:
The correct response is (B). We can plug in these values for “w” and “y” in the original equation:
(-1/x)(x)(1/z)(z) = -1. The x’s and z’s cancel out so that we get: (-1)(1) = -1. The answer will always be “Yes” no matter what the actual values are for w, x, y, and z. This is sufficient.
If you chose (A), remember this is a Y/N question. The stem does not tell us any information about what numbers w, x, y, and z are. This is a great question to pick numbers! As long as we can choose two sets of numbers: one that gives us an outcomes of “Yes” and the other that gives an outcome of “No,” we know the statement is insufficient.
Let’s choose w = 1, x = 1, y = 1, and z = -1. These numbers satisfy the condition in Statement (1) and allow us the answer the question “Yes.” However, if we chose w = 2, x = 2, y = 2, and z = -2, we would answer the question “No.” Therefore, this Statement must be insufficient.
If you chose (C), you may not have realized that we could substitute the value in Statement (2) to simplify wxyz = -1. By doing this, we realize that for ALL integers, b and d will cancel out leaving us with (-1)(1) = -1, which is always true.
If you chose (D), you correctly saw that substitution allows Statement (2) to be sufficient, but Statement (1) is not sufficient. Depending on what integers we select for the variables we can make their product equal or not equal to -1.
If you chose (E), you missed that Statement (2) is sufficient once we substitute it into the original equation. Sometimes statements will be unexpectedly sufficient in this way on the GMAT, even though we don’t know the actual values for the variables!
(-1/x)(x)(1/z)(z) = -1. The x’s and z’s cancel out so that we get: (-1)(1) = -1. The answer will always be “Yes” no matter what the actual values are for w, x, y, and z. This is sufficient.
If you chose (A), remember this is a Y/N question. The stem does not tell us any information about what numbers w, x, y, and z are. This is a great question to pick numbers! As long as we can choose two sets of numbers: one that gives us an outcomes of “Yes” and the other that gives an outcome of “No,” we know the statement is insufficient.
Let’s choose w = 1, x = 1, y = 1, and z = -1. These numbers satisfy the condition in Statement (1) and allow us the answer the question “Yes.” However, if we chose w = 2, x = 2, y = 2, and z = -2, we would answer the question “No.” Therefore, this Statement must be insufficient.
If you chose (C), you may not have realized that we could substitute the value in Statement (2) to simplify wxyz = -1. By doing this, we realize that for ALL integers, b and d will cancel out leaving us with (-1)(1) = -1, which is always true.
If you chose (D), you correctly saw that substitution allows Statement (2) to be sufficient, but Statement (1) is not sufficient. Depending on what integers we select for the variables we can make their product equal or not equal to -1.
If you chose (E), you missed that Statement (2) is sufficient once we substitute it into the original equation. Sometimes statements will be unexpectedly sufficient in this way on the GMAT, even though we don’t know the actual values for the variables!
Question 10 |
If the product of j and k does not equal zero, is j<0 and k>0?
(1) (-j, k) lies above the x-axis and to the right of the y-axis.
(2) (j, -k) lies below the x-axis and to the left of the y-axis.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient. | |
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient. | |
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient. | |
EACH statement ALONE is sufficient. | |
Statements (1) and (2) TOGETHER are NOT sufficient. |
Question 10 Explanation:
The correct response is (D). Each statement alone is sufficient.
Statement 1: If (-j, k) lie above the x-axis and to the right of the y-axis (that is, in the first quadrant), then we can write the following two inequalities: -j>0, and k>0 OR j<0 and k>0. Statement 1 is sufficient to answer the question.
Statement (2): If (j, -k) is in the third quadrant (as the information in statement 2 implies), then j = negative, and –k = negative.
We can write the following inequalities: j<0, and –k<0, OR j<0, and k>0. Statement 2 alone is sufficient to answer the question.
Statement 1: If (-j, k) lie above the x-axis and to the right of the y-axis (that is, in the first quadrant), then we can write the following two inequalities: -j>0, and k>0 OR j<0 and k>0. Statement 1 is sufficient to answer the question.
Statement (2): If (j, -k) is in the third quadrant (as the information in statement 2 implies), then j = negative, and –k = negative.
We can write the following inequalities: j<0, and –k<0, OR j<0, and k>0. Statement 2 alone is sufficient to answer the question.
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
More Practice Tests:
More Quantitative Tests>>
Integrated Reasoning Tests>>
Verbal Tests>>
Main Menu>>
