Directions: Solve the problem and select the best of the answer choices given.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Lady Edith bought several necklaces at the jewelry store, and each necklace cost 16 dollars. Lady Mary also purchased several necklaces, at a cost of $20 each. If the ratio of the number of necklaces Lady Edith purchased to the number of necklaces Lady Mary purchased is 3 to 2, what is the average cost of the necklaces purchased by Lady Edith and Lady Mary?
16.7 | |
17.1 | |
17.6 | |
17.9 | |
18.2 |
Question 1 Explanation:
The correct response is (C). For every 5 necklaces purchased by these ladies, 3 of them are Lady Edith’s and 2 of them are Lady Mary’s. We can set up an equation to find the total amount spent:
3(16) + 2(20) = Total Amount Spent for every 5 necklaces
88 = Total Amount Spent for every 5 necklaces
To find the average cost of the necklaces, we can simply divide 88 by 5. 88/5 = 17.6.
3(16) + 2(20) = Total Amount Spent for every 5 necklaces
88 = Total Amount Spent for every 5 necklaces
To find the average cost of the necklaces, we can simply divide 88 by 5. 88/5 = 17.6.
Question 2 |
Matthew, Jared, and Richard all bought flowers. The number of flowers Matthew purchased was equal to a single digit. Of the numbers of flowers purchased by Matthew, Jared, and Richard, only one was divisible by 3. The number of flowers one of them bought was an even number. Which of the following could represent the numbers of flowers each purchased?
3, 8, 24 | |
7, 9, 17 | |
6, 9, 12 | |
5, 15, 18 | |
9, 10, 13 |
Question 2 Explanation:
The correct response is (E). It is easier to use process of elimination on this type of question. Since all of the answer choices have at least one single-digit number in it, let’s look at the second requirement. If only one of the numbers was divisible by 3, we can eliminate answer choices that contain more than one multiple of 3: (A), (C), and (D).
The third requirement is that we have at least one even number. Between (B) and (E), only choice (E) contains an even number, 10.
The third requirement is that we have at least one even number. Between (B) and (E), only choice (E) contains an even number, 10.
Question 3 |
Circle P is inside Circle Q, and the two circles share the same center X. If the circumference of Q is four times the circumference of P, and the radius of Circle P is three, what is the difference between Circle Q’s diameter and Circle P’s diameter?
6 | |
9 | |
12 | |
18 | |
24 |
Question 3 Explanation:
The correct response is (D). Start by drawing the figure.
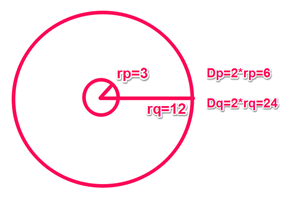
If the radius of P is 3, then its diameter is 6. Its circumference is 2πr = 6π. Q’s circumference is four times P’s circumference. Q’s circumference = 24π = 2πr. Q’s radius must be 12, and its diameter is 24.
The difference between the diameters is 24 – 6 = 18.

If the radius of P is 3, then its diameter is 6. Its circumference is 2πr = 6π. Q’s circumference is four times P’s circumference. Q’s circumference = 24π = 2πr. Q’s radius must be 12, and its diameter is 24.
The difference between the diameters is 24 – 6 = 18.
Question 4 |
A yellow taxi cab went from Downtown to the Beachside and back at an average speed of 2/3 miles per hour. If the distance from Beachside to Downtown is 1 mile, and the trip back took half as much time as the trip there, what was the average speed of the yellow taxi cab on the way to Beachside?
1/3 | |
1/2 | |
3/4 | |
2/3 | |
3/2 |
Question 4 Explanation:
The correct response is (B). It’s important to first understand what this question is asking. “On the way to Beachside” means the way there. The question is asking the average speed for a portion of the total trip. To find it, we’ll need to know the distance for that part of the trip and the time spent on that part of the trip.
If the average speed of the entire journey was 2/3 miles per hour, then every 3 hours 2 miles were travelled. Since the total distance was 2 miles, the total time must have been 3 hours. If the way back took half as much time as the way there, then for every 3 hours, 2 hours was spent on the way there, and 1 hour was spent on the way back.
Average Speed = Distance/Time = 1 mile / 2 hours. The average speed for the way to Beachside was ½ mph.
If the average speed of the entire journey was 2/3 miles per hour, then every 3 hours 2 miles were travelled. Since the total distance was 2 miles, the total time must have been 3 hours. If the way back took half as much time as the way there, then for every 3 hours, 2 hours was spent on the way there, and 1 hour was spent on the way back.
Average Speed = Distance/Time = 1 mile / 2 hours. The average speed for the way to Beachside was ½ mph.
Question 5 |
Circle B’s diameter was multiplied by 1.8. By what percent, approximately, was the area increased?
80% | |
125% | |
225% | |
325% | |
375% |
Question 5 Explanation:
The correct response is (C). This is a great question for plugging in your own values. Let’s say the value of the original radius was 10. The original area would be equal to πr2 = (10)2π = 100π. If the diameter increased by 80%, the new radius would be 18, and the new area would be equal to πr2 = (18)2π = 324π.
The increase is 324π - 100π = 224π. An increase of 224/100, or approximately 225%.
The increase is 324π - 100π = 224π. An increase of 224/100, or approximately 225%.
Question 6 |
What is the value of the square root of the square root of .00000256?
0.004 | |
0.016 | |
0.04 | |
0.16 | |
0.4 |
Question 6 Explanation:
The correct response is (C). To solve algebraically, start by taking the square root of .00000256. We know the square root of 256 = 16. We can write 0.00000256 in scientific notation as 256 x 10-8. So:
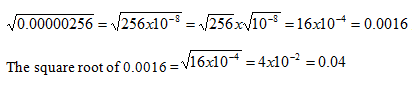
To double-check, you can backsolve:
04 x .04 = .0016, and .0016 x .0016 = .00000256.
If you chose (A), you miscalculated by one decimal point. Check your work by backsolving: .004 x .004 = .000016. And .000016 x .000016 = .000000000256 (four extra zeros).
If you chose (B), you need to take the square root twice. Zeros aside, the square root of 256 = 16, and the square root of 16 = 4.
If you chose (D), you miscalculated the zeros and you forgot to take the square root twice. If you backsolved to check your work you’d see that .16 x .16 = .0256. That result squared will not give us .00000256.
If you chose (E), you missed the correct choice by one decimal point. If you backsolved to check your work, you’d see that .4 x .4 = .16, and .16 x .16 = .0256, which is much larger than our original number from the question stem.
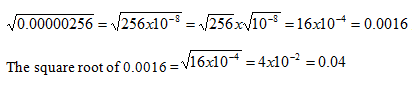
To double-check, you can backsolve:
04 x .04 = .0016, and .0016 x .0016 = .00000256.
If you chose (A), you miscalculated by one decimal point. Check your work by backsolving: .004 x .004 = .000016. And .000016 x .000016 = .000000000256 (four extra zeros).
If you chose (B), you need to take the square root twice. Zeros aside, the square root of 256 = 16, and the square root of 16 = 4.
If you chose (D), you miscalculated the zeros and you forgot to take the square root twice. If you backsolved to check your work you’d see that .16 x .16 = .0256. That result squared will not give us .00000256.
If you chose (E), you missed the correct choice by one decimal point. If you backsolved to check your work, you’d see that .4 x .4 = .16, and .16 x .16 = .0256, which is much larger than our original number from the question stem.
Question 7 |
Which of the following is NOT a possible value of
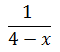
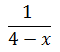
-4 | |
4/17 | |
0 | |
4 | |
17/4 |
Question 7 Explanation:
The correct response is (C). The denominator of any fraction is undefined when it equals 0, so x cannot be 4 in this expression. However, the question asks what cannot be a value for 1 / 4 – x. 1 divided by any number cannot equal zero.
If you chose (A), it is possible for 1 / 4 – x = -4 if x = 17/4.
If you chose (B), it is possible for 1 / 4 – x = 4/17 if x = -1/4.
If you chose (D), remember the question is asking what the expression can equal, not the possible values for x. This is a “trap” answer choice!
If you chose (E), it’s possible for 1 / 4 – x = 17/4 if x = 64/17.
If you chose (A), it is possible for 1 / 4 – x = -4 if x = 17/4.
If you chose (B), it is possible for 1 / 4 – x = 4/17 if x = -1/4.
If you chose (D), remember the question is asking what the expression can equal, not the possible values for x. This is a “trap” answer choice!
If you chose (E), it’s possible for 1 / 4 – x = 17/4 if x = 64/17.
Question 8 |
Which of the following numbers has the greatest number of unique digits?
1/6 | |
1/4 | |
1/3 | |
3/4 | |
5/7 |
Question 8 Explanation:
The correct response is (E). 5/7 = .7142…. Already there are more than four unique digits, which is more than any other number in the answer choices. Remember for each value there are only ten possible digits for each placeholder in a number: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The word “unique” means different from the other digits.
If you chose (A), 1/6 = .166666. There are only two unique digits in this number: 1 and 6.
If you chose (B), 1/4 = .25. There are only two unique digits in this number: 2 and 5.
If you chose (C), 1/3 = .333333. There is only 1 digit in this number: 3.
If you chose (D), 3/4 = .75. There are only two unique digits in this number: 7 and 5.
If you chose (A), 1/6 = .166666. There are only two unique digits in this number: 1 and 6.
If you chose (B), 1/4 = .25. There are only two unique digits in this number: 2 and 5.
If you chose (C), 1/3 = .333333. There is only 1 digit in this number: 3.
If you chose (D), 3/4 = .75. There are only two unique digits in this number: 7 and 5.
Question 9 |
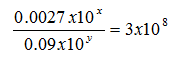 What is the value of y less than x?
What is the value of y less than x?
9 | |
10 | |
11 | |
12 | |
13 |
Question 9 Explanation:
To begin, we can translate “ y less than x” as “x – y.” Next, notice how the quotient is 3 x 108. Since “3” is the first part of this number written in scientific notation, let’s start by adjusting the scientific notation of the dividend and divisor (numerator and denominator) so we can achieve that 3.
.0027 / .09 might not equal 3, but 27/9 does, so we’ll have to adjust the exponent of each 10 as we move the decimal. 0.0027 x 10x = 27 x 10x - 4. When we move the decimal to the right, we must shrink the exponent of the 10 power. 0.09 x 10y = 9 x 10y - 2. Now we can rewrite the equation as 27 x 10x - 4 / 9 x 10y - 2 = 3 x 108. Separating out the powers of 10 we arrive at: 10x - 4 / 10y - 2 = 108. If you remember from the exponent rules, when we divide exponents with the same base, we subtract the exponents.
Thus, (x – 4) – (y -2) = 8.
x – 4 – y + 2 = 8
x – y – 2 = 8
x – y = 10
Even though we can’t solve for x and y independently, we found what the question was asking us to find, “x – y.” (B) is correct.
.0027 / .09 might not equal 3, but 27/9 does, so we’ll have to adjust the exponent of each 10 as we move the decimal. 0.0027 x 10x = 27 x 10x - 4. When we move the decimal to the right, we must shrink the exponent of the 10 power. 0.09 x 10y = 9 x 10y - 2. Now we can rewrite the equation as 27 x 10x - 4 / 9 x 10y - 2 = 3 x 108. Separating out the powers of 10 we arrive at: 10x - 4 / 10y - 2 = 108. If you remember from the exponent rules, when we divide exponents with the same base, we subtract the exponents.
Thus, (x – 4) – (y -2) = 8.
x – 4 – y + 2 = 8
x – y – 2 = 8
x – y = 10
Even though we can’t solve for x and y independently, we found what the question was asking us to find, “x – y.” (B) is correct.
Question 10 |
If x and y are positive integers, what percent of three more than y is twice the value of x?
1/200x(y + 3) | |
y + 3/200x | |
100(y + 3)/2x | |
(200x/y) + 3 | |
200x/(y + 3) |
Question 10 Explanation:
The correct response is (E). This is a great question to choose values for x and y. Let’s say x = 2. “Twice the value of x” would be 4. Now let’s say y = 5. “Three more than y” would be 8. The question is now asking: what percent of 8 is 4? We know that 4 is 50% of 8.
When we plug in our values into the answer choices, the correct response will also yield 50%: (200x/(y + 3) = 200(2) / (5) + 3 = 400/8 = 50. Always look for opportunities to pick numbers on the GMAT and avoid complicated algebra!
When we plug in our values into the answer choices, the correct response will also yield 50%: (200x/(y + 3) = 200(2) / (5) + 3 = 400/8 = 50. Always look for opportunities to pick numbers on the GMAT and avoid complicated algebra!
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
More Practice Tests:
More Quantitative Tests>>
Integrated Reasoning Tests>>
Verbal Tests>>
Main Menu>>
