Data Sufficiency Practice Test 1

The correct response is (A).

The first statement allows us to express the total number of children in the first two groups in terms of the number of children in the third group. Let’s call the smaller groups A and B, and the largest group C. Thus, we can express the first statement: A + B = C.

We know from the question-stem that A + B + C = 50
So we know C = 50 – (A + B).

Using substitution, C = 50 – C.
2C = 50
C = 25. Sufficient.

The second statement tells us the value of A, the smallest group.

This only tells us that 6 + B + C = 50. Without knowing B, we cannot determine a unique value for C.

The correct answer is (B).

(1) If it costs more than $1,000 annually to feed 4 raccoons, we do not have enough information to answer either yes or no to the original question. It could cost $2,000 to feed 4 raccoons, in which case it WOULD cost more than $2,000 to feed 7 raccoons. Or, it could cost only $1,000 and one cent to feed 4 raccoons, in which case feeding 3 more would be less than an additional $1,000, and the answer would be no. This statement is insufficient.

(2) If it costs more than $1,500 annually to feed 5 raccoons, then the smallest cost for each animal is a little over $300. $300 x 7 raccoons = $2,100. Sufficient.

The correct response is (D).

The missing information here is the value of s. Both statements allow us to find s. Statement (1) allows us to do so by simplifying and solving the equation for s. From Statement (2) we know we can find “z” from the information given in the question stem. Once we find z, we can plug in for s. From the question stem we can calculate z% as follows:

Simple interest = principal x rate x time. $450 = $8000 * z/100 * 1, so z = 5.625%. Now that we know z, we can plug in to solve for s in Statement (2).

The correct response is (C).

(1) If no additional voters are added to the bloc, and 4 of the current voters leave the bloc, there will be fewer than 20 voters.

We can translate the given information into an inequality: x – 4 < 20, where “x” is the number of current voters. We know x < 24, but we cannot determine an exact value for x.

(2) If 4 more voters join the bloc and all of the present voters remain, there will be at least 27 voters.

We can translate the given information into an inequality: x + 4 ≥ 27. “At least” means there could be 27 OR more than 27 in the bloc. This inequality simplifies to x ≥ 23. We do not know the exact value of x based on this inequality.

Combining both statements we know 23 ≤ x < 24. If x must be less than 24, but greater or equal to 23, the only number that satisfies both conditions is 23.

If you chose (D), keep in mind that each statement alone only allows us to limit the range of possible values for “x,” but not find the actual numerical value. For a “value” DS question, if more than one number is possible, the statement cannot be sufficient.

If you chose (E), you may not have realized that we could have expressed the information in the statements as inequalities. Both statements combined then allow us to limit the range of possible values to one, so combined they are sufficient.

The correct response is (B).

(1) 7y is an integer.

If you chose (A), note that it is possible for 7y to be an integer when y is an integer. For example, if y = 1, 7y = 7. However, it is also possible for 7y to be an integer when y is not an integer. For example, if 7y = 1, then y =1/7.

(2) y/7 is an integer.

If y/7 is an integer, then y must be a multiple of 7. All multiples of 7 are themselves integers (7, 14, 21, etc.).

If you chose (C), you failed to recognize that Statement (2) was sufficient by itself, as there is no value we can choose for y that makes y/7 an integer that is not itself an integer. Picking numbers can help you see this relationship more clearly.

The correct answer is (E).

If you chose (A), from Statement 1, the possible values for the digits are 0 and 5, 1 and 4, or 2 and 3. So the possible numbers are: 50, 14, 41, 23, or 32. We don’t know which of these is x.

If you chose (B), from Statement 2, we know x is prime, but there are many two-digit prime numbers: 11, 13, 17, 19, etc.

If you chose (C), remember that both 23 and 41 are prime numbers.

If you chose (D), both statements offer limiting information, but because this is a “value” question, a statement can only be considered sufficient if it allows us to limit our range of possible x’s to ONE value only.

The answer is (E). Statement 1 limits our possible x’s to 5 integers, and Statement 2 narrows that list to 2 integers. However, we still do not know whether x is 23 or 41.

The correct response is (B).

We know from the question that each family member got at least 1 present, that they all got the same number of presents, and that no presents were left over. Based on this information, we can write the following inequality:

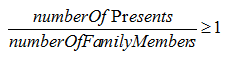
(1) The first statement would be useful if we needed to know the number of family members, but it doesn't help to answer this yes/no question.

(2) Based on the information in statement (2), we can write the following inequality:

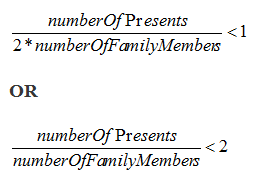
Combining the information in statement (2) and the information in the question stem, we find that:

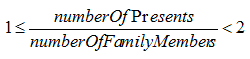
Since each family member got at least one present, and the number of presents per family member is less than 2, we can conclude that each family member received only one present.

The answer to the original question is NO. However, if we can answer YES/NO to a data sufficiency question based on the information in a statement, then that statement is sufficient. Statement (2) is sufficient.

The correct response is (D).

Statement (1) is sufficient. If the box is 18 inches long and 9 cylinders fit along that length, then they must each have a diameter of 2.

Statement (2) is also sufficient. In order to find the value of x, we need to know the diameter of each cylinder. This is given by Statement (2), since twice the radius of the ball bearing will equal the cylinder’s diameter. If each cylinder has a diameter of 2, then 9 will fit along the length of the box and 5 will fit along the width. A total of 9 x 5 = 45 cylinders will fit inside the box.

The correct response is (C).

To find the number of girls who are members of BOTH teams, we must find the overlap of this set. From Statement (1), we know that there are 18 girls total. Some are members of the Diving Team-only, some are members of the Swim Team-only, and some are members of both. But we do not have enough information to determine the number of girls who are members of both teams. Statement (1) alone is not sufficient.

From Statement (2), we know that 1/3 of the 27 Diving Team members are girls, so there are 9 girls in the Diving Team. We’re also told that 1/2 of the 24 Swim Team members are girls, so there are 12 girls in the Swim Team. Combined, that is a head-count of 9 + 12 = 21 girls. However, we still cannot determine how many girls are members of both teams. Statement (2) alone is not sufficient.

Combining both statements, we know that there are only 18 girls total who are members of these two clubs. Therefore, the extra 3 girls from our “headcount” must come from the number of girls who are members of both clubs.

The correct response is (B).

Statement (1) says that JK < 1. In order for this to be true, at least one of these numbers must be a positive fraction. We can quickly choose numbers to test this: If J = 1 and K = ½, their product is ½ and this less than 1. In this case, the answer to the question would be “YES” since 1 ÷ ½ = 2, which is greater than 1. But what if J = ½ and K = 1? J/K would be equal to ½. In this case, the answer to the question would be “NO”. Since the answer to the question can be “YES” or “NO” depending on the values of J and K, Statement (1) alone is not sufficient to answer the question.

Statement (2) tells us that J – K > 0. Let’s quickly choose values again. If J = 1 and K = ½, we satisfy the statement and get a “YES” answer. In fact, for all values we choose we will get a “YES” since J – K > 0 can be manipulated to read J > K. If J is always greater than K, then J/K will always be greater than 1. Statement (2) Alone is sufficient to answer the question.