The GMAT Problem Solving questions will test your ability to evaluate information and solve numerical problems. Our practice problems are designed to be very challenging in order to prepare you for the harder-level questions found on the GMAT. Answers and detailed explanations are include with each problem. Start your test prep now with our free GMAT Problem Solving practice test.
Directions: Solve the problem and select the best of the answer choices given.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The City Opera House is expanding. Currently the city block containing the opera house is rectangular-shaped with a total volume of 9600 feet. If the expanded Opera House is 2.5 times as long, wide, and deep as the original building, what would the new volume be?
24,000 | |
60,000 | |
72,000 | |
150,000 | |
245,000 |
Question 1 Explanation:
The correct response is (D). The volume is the length x width x height. The building’s original volume is equal to lwh = 9600. The new footage will be 2.5l x 2.5w x 2.5h, or (lwh) x 2.5 x 2.5 x 2.5 = 15.625(lwh). Since lwh = 9600, the new volume will be 15.625(9600) = 150,000.
Question 2 |
In a university club of 200 people, the number of Political Science majors is 50 less than 4 times the number of International Relations majors. If one fifth of the club members are neither Political Science majors nor International Relations majors, and no club member is majoring in both Political Science and International Relations, how many of the club members are International Relations majors?
42 | |
50 | |
71 | |
95 | |
124 |
Question 2 Explanation:
The correct response is (A). Let P be the number of Political Science majors and let R be the number of International Relations majors. "One fifth of the legislators are neither," so there are 1/5 *200 = 40 legislators who are neither. Hence, there are 200 – 40 = 160 Poly-Sci majors and IR majors, or P + R = 160. Translating the clause "the number of Poly-Sci majors is 50 less than 4 times the number of IR majors" into an equation yields P = 4R – 50.
Plugging this into the equation P + R = 160 yields:
4R – 50 + R = 160
5R – 50 = 160
5R = 210
R = 42
Plugging this into the equation P + R = 160 yields:
4R – 50 + R = 160
5R – 50 = 160
5R = 210
R = 42
Question 3 |
If the total cost of 20 pairs of shoes is equal to the total revenue generated from the sale of 25 pairs of shoes, what is the percent of profit or loss made on the sale of each pair of shoes, assuming each pair of shoes cost the same dollar amount and each pair of shoes sold for the same dollar amount?
25% loss | |
25% profit | |
20% loss | |
20% profit | |
5% profit |
Question 3 Explanation:
The correct response is (C). The need-to-know formula here is: Profit/Loss % = (Sales Price – Cost Price) / Cost Price x 100. The stem tells us that 20c = 25s, or 4c = 5s, so the ratio of the sales price to the cost price is 4/5.
Let’s simplify our Profit/Loss % formula by dividing each term by the cost price: Profit/Loss % = (S/C – C/C) x 100
P/L% = (S/C – 1) x 100 We know that S/C = 4/5 for this problem. So we can plug in and solve:
P/L% = (4/5 – 1) x 100
P/L% = (-1/5) x 100
P/L% = -20%. The answer is a 20% loss.
Let’s simplify our Profit/Loss % formula by dividing each term by the cost price: Profit/Loss % = (S/C – C/C) x 100
P/L% = (S/C – 1) x 100 We know that S/C = 4/5 for this problem. So we can plug in and solve:
P/L% = (4/5 – 1) x 100
P/L% = (-1/5) x 100
P/L% = -20%. The answer is a 20% loss.
Question 4 |
Clarissa spent all day on a sightseeing trip in Britain. Starting from her hotel, Clarissa boarded a bus, which traveled at an average speed of 15 miles per hour through a 30 mile section of the countryside. The bus then stopped for lunch in London before continuing on a 3 hour tour of the city's sights at a speed of 10mph. Finally, the bus left the city and drove 40 miles straight back to the hotel. Clarissa arrived at her hotel exactly 2 hours after leaving London. What was the bus's average rate, approximately, for the entire journey?
8 | |
14 | |
21 | |
25 | |
30 |
Question 4 Explanation:
The correct response is (B). To find the "Average Rate" of the bus, we know we will need to find the Total Distance and the Total Time, so let's see how we can use the D = R x T formula to find the missing info.
For the first part of the trip, we know that 30 miles = 15mph x T, so we know that T = 2 hours. For the middle part of the trip, we know that D = 10mph x 3 hours, so we know that D = 30 miles. For the last part of the trip, we know that 40 miles = R x 2 hours, so we know that R = 20mph.
Now we can find the Total Distance and the Total Time. Total Distance = 30 miles + 30 miles + 40miles = 100 miles. Total Time = 2 hours + 3 hours + 2 hours = 7 hours. So the Average Rate = 100 miles/ 7 hours = 14.28mph. (B) is the closest approximation.
For the first part of the trip, we know that 30 miles = 15mph x T, so we know that T = 2 hours. For the middle part of the trip, we know that D = 10mph x 3 hours, so we know that D = 30 miles. For the last part of the trip, we know that 40 miles = R x 2 hours, so we know that R = 20mph.
Now we can find the Total Distance and the Total Time. Total Distance = 30 miles + 30 miles + 40miles = 100 miles. Total Time = 2 hours + 3 hours + 2 hours = 7 hours. So the Average Rate = 100 miles/ 7 hours = 14.28mph. (B) is the closest approximation.
Question 5 |
Meredith jogged to the top of a steep hill at an average pace of 6 miles per hour. She took the same trail back down. To her relief, the descent was much faster; her average speed rose to 14 miles per hour. If the entire run took Meredith exactly one hour to complete and she did not make any stops, how many miles, approximately, is the trail one way?
2 | |
3 | |
4 | |
5 | |
6 |
Question 5 Explanation:
The correct response is (C).
Time = Distance/Rate
Time spent going uphill = D /6
Time spent going downhill = D/14
Total Time = 1 hour
We can write the following equation, and solve for D:
Time taken on the uphill journey + Time taken on the downhill journey = Total Time
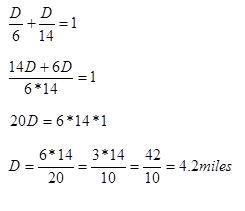
Time = Distance/Rate
Time spent going uphill = D /6
Time spent going downhill = D/14
Total Time = 1 hour
We can write the following equation, and solve for D:
Time taken on the uphill journey + Time taken on the downhill journey = Total Time
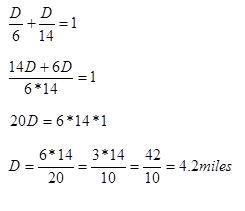
Question 6 |
At a medical research lab, nine doctors are conducting multiple clinical trials. Six of the doctors are working on a clinical trial with exactly one other doctor and three doctors are working on a clinical trial with exactly two other doctors. If two doctors are selected at random from the lab, what is the probability that those two doctors are NOT working together on a clinical trial?
1/12 | |
2/12 | |
5/12 | |
7/12 | |
10/12 |
Question 6 Explanation:
The correct response is (E). Remember that the probability of something NOT occurring is 1 – the probability of it occurring. So for this question, we can find the probability that those two doctors WILL be working together, then subtract it from one. Let’s start with the first group. If the first person we chose was from the first group, the odds that the second person would be their partner would be 1/8. This is because every doctor in the first group only has ONE partner, and we’d have 8 people to choose from after picking the first person (out of 9 total). 6/9*1/8 = 6/72 = 1/12.
If the first person we chose was from the second group (probability = 3/9), the odds that the second person would be one of their partners would be 2/8. The numerator is 2 this time because each person in the second group has two partners instead of one. 3/9*2/8 = 6/72 = 1/12.
Since EITHER of these outcomes (picking the first person from the first group OR the second group) produces our desired result, we’ll add these probabilities. 1/12 + 1/12 = 2/12 = 1/6.
Therefore, the probability that the two doctors are NOT working together is 1 – 1/6 = 5/6.
Another way to think of this question is to assign letters to each doctor and group them by clinical trial. So AB, CD, EF are from the first group, and GHI are from the second group. There are 6 ways of choosing a pair that are working together: AB, CD, EF, GH, GI, or HI. And we can quickly use the combination formula to find the total possible ways to choose 2 from 9. 9C2 = 9! / 2! 7! = 9 x 8/2 = 72/2 = 36. 6/36 = 1/6.
If the first person we chose was from the second group (probability = 3/9), the odds that the second person would be one of their partners would be 2/8. The numerator is 2 this time because each person in the second group has two partners instead of one. 3/9*2/8 = 6/72 = 1/12.
Since EITHER of these outcomes (picking the first person from the first group OR the second group) produces our desired result, we’ll add these probabilities. 1/12 + 1/12 = 2/12 = 1/6.
Therefore, the probability that the two doctors are NOT working together is 1 – 1/6 = 5/6.
Another way to think of this question is to assign letters to each doctor and group them by clinical trial. So AB, CD, EF are from the first group, and GHI are from the second group. There are 6 ways of choosing a pair that are working together: AB, CD, EF, GH, GI, or HI. And we can quickly use the combination formula to find the total possible ways to choose 2 from 9. 9C2 = 9! / 2! 7! = 9 x 8/2 = 72/2 = 36. 6/36 = 1/6.
Question 7 |
For which of the following functions g is g(z) = g(1 – z) for all z?
g(z) = 1 - z | |
g(z) = 1 – z2 | |
g(z) = z2 – (1 – z)2 | |
g(z) = z2(1 – z)2 | |
g(z) = z / 1-z |
Question 7 Explanation:
The correct response is (D). For questions with functions in the answer choices, use the given definitions to check each of the answer choices. For instance, since we want f(z) = f(1-z) we can assume z=4, and check each of the answer choices to see if f(4) = f(1-4), or, f(4) = f(-3).
If you notice that, then it very easy to find the solution, replace each function with 4 and -3 instead of z, and see if f(4)=f(-3).
Let’s try choice (A):
F(-3) = 1 – (-3) = 4
F(4) = 1 - (4) = -3
They are NOT equal. Eliminate.
Repeat this process for the other answer choices, until you find one for which f(4) = f(-3). That choice is D:
F(-3) = (-3)2 (1 – (-3))2 = (9)(16)
F(4) = (4)2 (1 – (4))2 = (16)(9)
F(-3) = F(4).
If you notice that, then it very easy to find the solution, replace each function with 4 and -3 instead of z, and see if f(4)=f(-3).
Let’s try choice (A):
F(-3) = 1 – (-3) = 4
F(4) = 1 - (4) = -3
They are NOT equal. Eliminate.
Repeat this process for the other answer choices, until you find one for which f(4) = f(-3). That choice is D:
F(-3) = (-3)2 (1 – (-3))2 = (9)(16)
F(4) = (4)2 (1 – (4))2 = (16)(9)
F(-3) = F(4).
Question 8 |
A right triangle has sides that are consecutive even integers. The longest side is z. Which of the following equations could be used to find z?
(z – 4)2 = z2 – (z - 2)2 | |
(z – 2)2 = (z – 4) – z2 | |
z2 + 42 + 22 = 62 | |
(z – 2)2 = z2 – (z - 1)2 | |
(z + 2)2 + (z + 4)2 = z2 |
Question 8 Explanation:
The correct response is (A).
If we know the longest side is “z,” we can label the other two sides as “z-4” and “z-2” respectively because we know that “consecutive even” means each side differs from its next-largest neighbor by 2. For example: 6, 8, 10.
We would use the Pythagorean Theorem to find the value of z:
a2 + b2 = c2
(z – 2)2 + (z – 4)2 = z2
Remember that “c” is always the hypotenuse, or the longest side. Only choice (A) matches this equation.
We would use the Pythagorean Theorem to find the value of z:
a2 + b2 = c2
(z – 2)2 + (z – 4)2 = z2
Remember that “c” is always the hypotenuse, or the longest side. Only choice (A) matches this equation.
Question 9 |
Rectangle LMNO is inscribed in a circle with center P. If the area of the rectangle is 8 times its width, and the distance from P to side LM is 3, what is the circle’s approximate circumference?
5 | |
10 | |
30 | |
45 | |
75 |
Question 9 Explanation:
The correct response is (C). To find the circumference of a circle, we must find the radius. Let’s start with what we know:
The area of a rectangle is lw. Here we are told that lw = 8w. That means the length is 8. We also know that the distance from P to LM = 3, so the length of the rectangle must be 6. Let’s re-draw the shape:
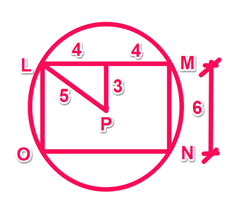
The radius of the circle, LP, is the hypotenuse of a right triangle whose other two sides are half the length and half the width of the rectangle. Since it’s a classic Pythagorean triplet (3:4:5), we don’t need to use the Pythagorean theorem.
Plug the radius into the formula for circumference: C = 2πr. C = 2*π*5. The circumference is approximately 10π, or a number slightly larger than 30.
The area of a rectangle is lw. Here we are told that lw = 8w. That means the length is 8. We also know that the distance from P to LM = 3, so the length of the rectangle must be 6. Let’s re-draw the shape:

The radius of the circle, LP, is the hypotenuse of a right triangle whose other two sides are half the length and half the width of the rectangle. Since it’s a classic Pythagorean triplet (3:4:5), we don’t need to use the Pythagorean theorem.
Plug the radius into the formula for circumference: C = 2πr. C = 2*π*5. The circumference is approximately 10π, or a number slightly larger than 30.
Question 10 |
Larry’s Lawn Service charges $w/hour for the first x hours of grass trimming, then w + 2 dollars for every hour of work over x hours. How much more will a homeowner be charged for a grass trimming job that took z hours if z > x than for a job which took only w hours if x < w < z?
x(z + w) | |
(w + 2) – zx | |
(w + 2) (z – w) | |
xw + 2 – (z – w) | |
w(x + z) + x |
Question 10 Explanation:
The correct response is (C). We can solve this problem by picking numbers:
We want x < w < z. Let’s pick x=3, w=4, z=6
For a job that took 4 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last hour. The total cost would be $4(3) + $6(1) = $12 + $6 = $18.
For a job that took 6 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last three hours. The total cost would be $4(3) + $6(3) = $12 + $18 = $30. The difference in price is $12.
Let’s plug our values into the expression: (w+2)(z-w) = (4+2)(6-4) = 6*2 = 12.
Here is the algebraic solution:
If the grass trimming job took z hours, the total cost is: wx + (z-x)(w+2)
If the grass trimming job took w hours, where x < w < z, the total cost is: wx + (w-x)(w+2)
The extra cost will be:
[wx + (z-x)(w+2)] – [wx + (w-x)(w+2)]
= (z-x)(w+2) - (w-x)(w+2)
= (w+2)[(z-x) – (w-x)]
= (w+2)(z-w)
We want x < w < z. Let’s pick x=3, w=4, z=6
For a job that took 4 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last hour. The total cost would be $4(3) + $6(1) = $12 + $6 = $18.
For a job that took 6 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last three hours. The total cost would be $4(3) + $6(3) = $12 + $18 = $30. The difference in price is $12.
Let’s plug our values into the expression: (w+2)(z-w) = (4+2)(6-4) = 6*2 = 12.
Here is the algebraic solution:
If the grass trimming job took z hours, the total cost is: wx + (z-x)(w+2)
If the grass trimming job took w hours, where x < w < z, the total cost is: wx + (w-x)(w+2)
The extra cost will be:
[wx + (z-x)(w+2)] – [wx + (w-x)(w+2)]
= (z-x)(w+2) - (w-x)(w+2)
= (w+2)[(z-x) – (w-x)]
= (w+2)(z-w)
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 10 questions to complete.
|
List |
Next Practice Test:
Problem Solving Practice Test 2>>
More Practice Tests:
More Quantitative Tests>>
Integrated Reasoning Tests>>
Verbal Tests>>
Main Menu>>
